立体角（电动力学知识补充）

——写于

前言

上学期我在学电磁学的时候，就对这个立体角不太清楚，但是当时就囫囵吞枣过去了。结果这学期学电动力学，又遇到这个问题了，截图如下：

《电动力学》（第四版）郭硕鸿 第5页：

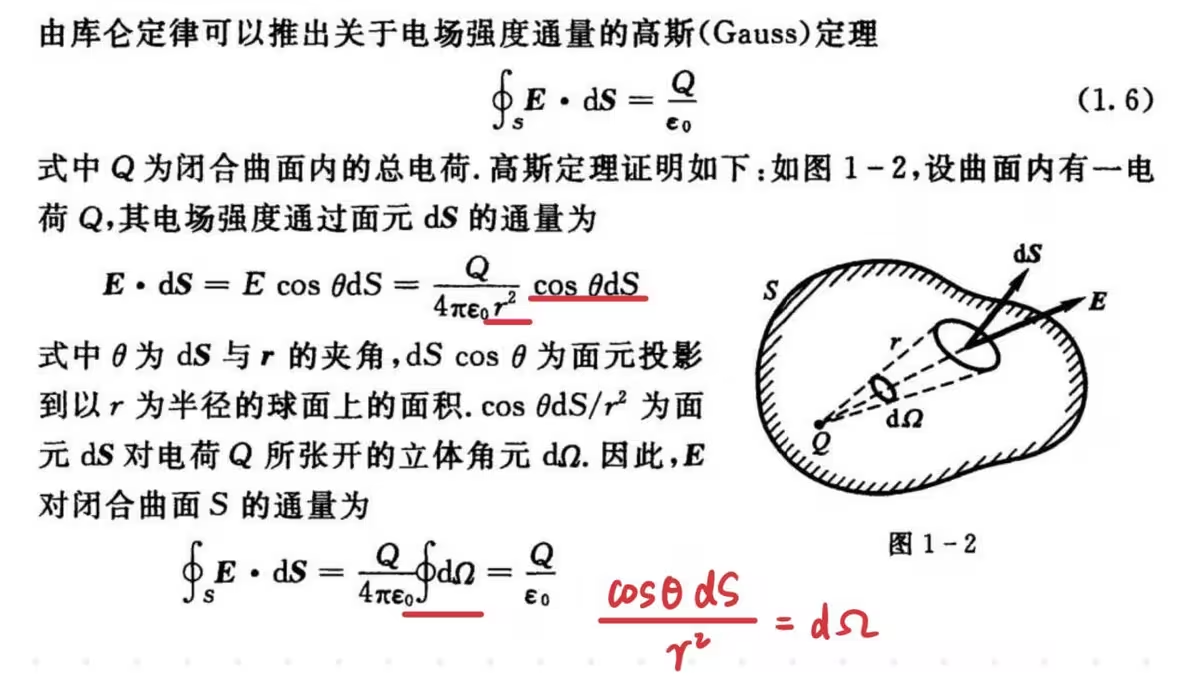
可以看到非常的amazing啊，一个立体角竟然表示成了两种形式——带了 的，和不带的（从直观上来说是这样的）。于是我上网查询了资料，将立体角的知识补充如下：

正文

对于二维平面的圆，我们有 ，微分形式为 ，对于全空间积分可得

对于三维空间的球，我们有 ，微分形式为 ，对于全空间积分可得

立体角的单位是球面度（steradian，sr）

在我看来，这个立体角是人为定义的用来度量空间角度的量——即用“从一个点向外延伸的射线或线段所覆盖的空间范围”来描述一个三维的角度，而除以 r^2 纯粹是为了积分之后能把 r^2 约掉，让它变成一个无量纲的量

而至于为什么前面有的公式出现了 ，而有的公式则没有出现——这是因为，如果我们选择的这个包围 点的曲面不是一个球面，而是一些不规则的封闭曲面的话，这时候就需要让曲面微元 和径矢 点乘作投影

于是立体角的矢量形式可以写成

而同样的，平面角也可以写成矢量的形式，依葫芦画瓢即可，我这里就懒得打公式了

补充

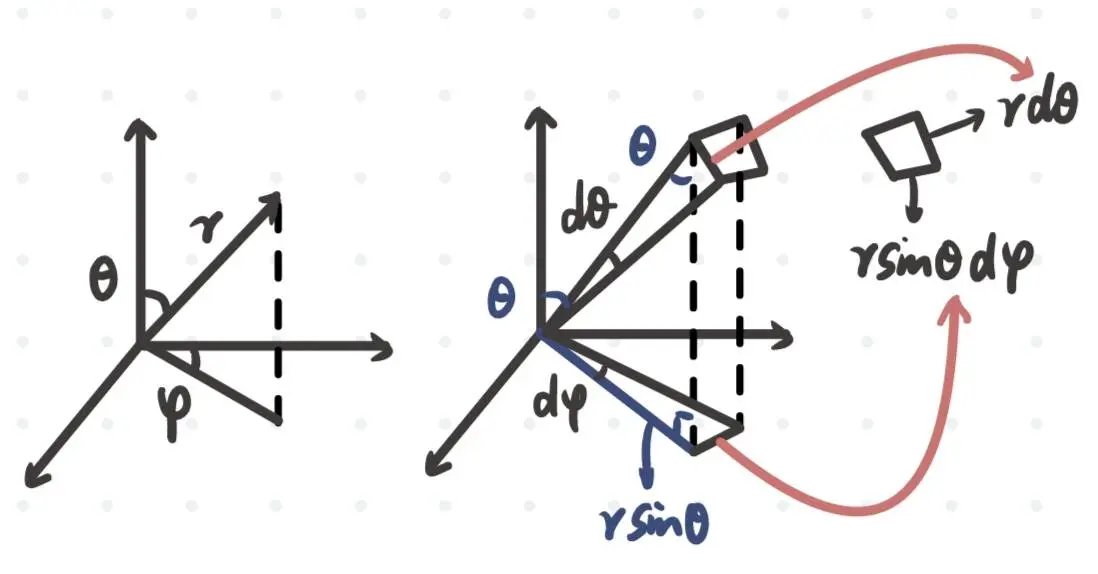
在球坐标系下有：

则立体角可表示为：

关于球坐标系下 的推导如下图所示：